class 12 physics chapter 4 important questions

Dear students class 12 physics chapter 4 important questions short answer type answers PDF have been collected at one place to get you all prepared for your 12th Bihar board exam, as well as for UP board exams ,Jharkhand board exam ,MP board exams ,Rajsthan board exams ,cbse board exams and other board exams. Visit my nawendu classes youtube channel for more help .

हिन्दी में पढ़ें

Q.(1)- Current carrying solenoid is used as a bar-magnet. Describe it.

Answer-

Current carrying solenoid as a bar-magnet

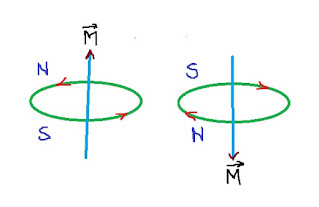
A current carrying solenoid produces magnetic field resemble to magnetic field of a bar magnet. The end of the current carrying solenoid where direction of current is clockwise acts as a south pole and the end of the current carrying solenoid where direction of current is anticlockwise acts as a north pole. So current carrying solenoid is used as a bar magnet.

Q.(2)- What is Lorentz force?

Bihar Board -2019 ,2022

Answer- Force on a charged particle placed in an electric and a magnetic field simultaneously is called Lorentz force.
If q charge is placed in electric field $\vec{E}$

then electric force on the charged particle

\[{{F}_{e}}=qE\]

\[{{\vec{F}}_{e}}=q\vec{E}\]

If q charge is placed in magnetic field $\vec{B}$

then magnetic force on the charged particle

${{F}_{m}}=qVB\sin \theta $

${{\vec{F}}_{m}}=q(\vec{V}\times \vec{B})$

Where v = velocity of the charged particle

\[\theta \]= angle between velocity of the charged particle and magnetic field

If q charge is placed in an electric and a magnetic both fields simultaneously then net force on the charged particle

$\vec{F}={{\vec{F}}_{e}}+{{\vec{F}}_{m}}$

$\vec{F}=q\left[ \vec{E}+\left( \vec{V}\times \vec{B} \right) \right]$

This is Lorentz Force.

Q.(3)- Write Fleming’s left hand rule.

Bihar Board -2020,2023

Answer- Three fingers of left hand thumb ,index finger and middle fingers are stretched mutually perpendicular . If index finger represents the direction of magnetic field, middle finger represents the direction of current then thumb will represent the direction force on(or motion of) the conductor.

Q.(4)- Cylindrical magnetic poles are used in a galvanometer ,Why?

Magnetic poles of a galvanometer are cylindrical (concave) why?
Answer- Cylindrical magnetic poles are used in a galvanometer to keep its coil always in radial position. Due to which torque on the coil is
maximum, which is equal to nIAB .

Q.(5)- What is shunt ?

Bihar Board -2019

Write two uses of shunt.

Bihar Board -2015, 2019

Answer- Shunt is a low resistance conductor ,which is connected parallel to a galvanometer or an ammeter to protect it from excess of current .

Uses of shunt-

(i) Shunt is used to protect a galvanometer or an ammeter from excess of current.

(ii) Shunt is used to convert a galvanometer into an ammeter .

(iii) Shunt is used to increase the range of an ammeter.

Q.(6)- What is difference between an ammeter and a voltmeter?

Answer- Ammeter
(i) Current is measured by ammeter.
(ii) Ammeter is connected in series
(iii) Its resistance is low.
Voltmeter
(i) potential difference is measured by voltmeter.
(ii) voltmeter is connected in parallel
(iii) Its resistance is high.

Q.(7)- What type of force acts between two mobile charges?

Answer- If two charges are stationary then electric force acts between them.
But, if two charges are mobile then electric and magnetic both forces act between them.
Q.(8)- Write the force between two parallel currents.
Answer- $F=\frac{{{\mu }_{o}}}{2\pi }\frac{{{I}_{1}}{{I}_{_{2}}}}{r}l$
Q.(9)- Why ammeter is connected in series, while voltmeter in parallel with main supply?
Answer- Ammeter is used to measure current. So it is connected in series so that whole current flows through it.
Voltmeter is used to measure potential difference between two points (of the circuit) therefore it is connected in parallel to those two points.
Q.(10)- How will you change an ammeter into voltmeter?
Answer- At first we will remove shunt from it then connect a high resistance in series with it to change it into a voltmeter.

Q.(11)- What is Bohr magneton ?

Answer- Bohr magneton is a small unit of magnetic dipole moment.

\[{{m}_{B}}=\frac{eh}{4\pi m}=9.27\times {{10}^{-24}}J/T\]

Q.(12)- Applying Biot-savart’s law deduce the expression the for the magnetic field at center of a semicircular loop of radius R carrying current I .

Bihar Board -2009

Answer-

Applying Biot-savart’s law deduce the expression the for the magnetic field at center of a semicircular loop of radius R carrying current I .

Let, there is a semicircular current carrying coil of radius R carrying current I.

dl is an small element of the circular coil.

The magnetic field at the center O of the coil due to the small element dl is dB.

A/C to Biot-Savart law

$dB=\frac{{{\mu }_{0}}}{4\pi }\times \frac{Idl\sin {{90}^{\circ }}}{{{R}^{2}}}$

$dB=\frac{{{\mu }_{0}}}{4\pi }\times \frac{Idl}{{{R}^{2}}}....\left( i \right)$

Now , magnetic field due to the whole semiconductor coil .

$B=\int{dB=\int\limits_{0}^{\pi R}{\frac{{{\mu }_{0}}}{4\pi }}}\times \frac{Idl}{{{R}^{2}}}$

\[B=\frac{{{\mu }_{0}}}{4\pi }\times \frac{I}{{{R}^{2}}}\int\limits_{0}^{\pi R}{dl}\]

\[B=\frac{{{\mu }_{0}}}{4\pi }\times \frac{I}{{{R}^{2}}}\left[ l \right]_{0}^{\pi R}\]

\[B=\frac{{{\mu }_{0}}}{4\pi }\times \frac{I}{{{R}^{2}}}\left[ \pi R-0 \right]\]

\[B=\frac{{{\mu }_{0}}}{4\pi }\times \frac{I}{{{R}^{2}}}\times \pi R\]

\[B=\frac{{{\mu }_{0}}I}{4R}\]

This is magnetic field at the center of the given semi circular coil .

Q.(13)- Write Biot- savart's law.

Bihar Board - 2021

Answer- Read in Nawendu Physics Classes notes.

Q.(15)- Explain behavior of a current loop as a magnetic dipole.

Bihar Board - 2009

Answer- The face (plane) of the current loop, where direction of current is clockwise , acts as a south pole and the face (plane) of the current loop, where direction of current is anti-clockwise , acts as a north pole.

Thus in a current loop very closed magnetic north - south poles are present so a current loop acts as a magnetic dipole.